Гид по Анализаторам Спектра
- Автор темы GrinGrin
- Дата начала
Мне кажется, что такое спектроанализатор знают многие!!!
Большенству обывателей интереснее познать практическое применение этих теоретических знаний! Например, как должен выглядеть микс, какой более приемлимый "рисунок" баса в диапазоне от 35ти до 80ти герц, какой энергией должны обладать хайхэты, итд, итп....
От себя скажу что эффективней настроить эквалайзер для просмотра спектра от 30ти до 17ти килогерц, чтобы "полезное" пространство максимально увеличилось...
Лично мне нравятся возможности визувлизации вэйвлаба! FFT показывает красной полосочкой основной спектр, а маленькими точками пики!! его можно растянуть на весь экран, имеются все необходимые настройки :bb:
Также нравится спектр в Adobe Audition...очень наглядно и интуитивно понятно!
В 7ом Аблетоне встроен отличный "Spectrum"!!! Можно также на весь экран развернуть, показывает аш до -180 dB :bb: имеются пресеты))))
Большенству обывателей интереснее познать практическое применение этих теоретических знаний! Например, как должен выглядеть микс, какой более приемлимый "рисунок" баса в диапазоне от 35ти до 80ти герц, какой энергией должны обладать хайхэты, итд, итп....
От себя скажу что эффективней настроить эквалайзер для просмотра спектра от 30ти до 17ти килогерц, чтобы "полезное" пространство максимально увеличилось...
Лично мне нравятся возможности визувлизации вэйвлаба! FFT показывает красной полосочкой основной спектр, а маленькими точками пики!! его можно растянуть на весь экран, имеются все необходимые настройки :bb:
Также нравится спектр в Adobe Audition...очень наглядно и интуитивно понятно!
В 7ом Аблетоне встроен отличный "Spectrum"!!! Можно также на весь экран развернуть, показывает аш до -180 dB :bb: имеются пресеты))))
выкладываю лучший по моему мнению анализатор с самым вменяемым откликом и детализацией, и в то же время не жрущий особо ресурсов.
SEKD Sonoscope (на самом деле очень редкая софтина. на офф сайте никакого упоминания
SEKD Sonoscope (на самом деле очень редкая софтина. на офф сайте никакого упоминания
Ну, что же, GrinGrin, когда же обещанное продолжение-то появится? Устали ждать уже. Уж прошло две недели от момента как Вы сказали: - "Думаю, что в течении трех дней будет готова вторая часть Гида". :wink2:
А я буду счаслив узная побольше (точнее, хоть что-то) о режимах отображения Hanning, Hamming, Blackman и им подобных в чём заключается разница, и в каких случаях более применимы.
Уже благодарен.
Так-же поддерживаю предпочтения IXL inspector, Span, Pinguin(standalone) и ещё не упомянутый Visualizer от NuGenAudio, в одном имеющий несколько анализаторов(Level meter, Spectrum analyzer, Spectrogram, Vectorscope, Phase analysis, Stereoscope, Stereo bias meter, Correlation meter) и ряд настроек к каждому.
Уже благодарен.
Так-же поддерживаю предпочтения IXL inspector, Span, Pinguin(standalone) и ещё не упомянутый Visualizer от NuGenAudio, в одном имеющий несколько анализаторов(Level meter, Spectrum analyzer, Spectrogram, Vectorscope, Phase analysis, Stereoscope, Stereo bias meter, Correlation meter) и ряд настроек к каждому.
Последнее редактирование модератором:
http://www.plus24.net/sekd/products/software.aspSEKD Sonoscope (на самом деле очень редкая софтина. на офф сайте никакого упоминания
Когда к сигналу применяется FFT, сигнал раскладывается не на те индивидуальные частоты, которые он содержит, а на фиксированный ряд частот, определяемый самим преобразованием FFT. Например, анализируем ноту 240 Гц + гармоники на частоте дискретизации 48 кГц и при размере окна FFT 4096 точек. Хотелось бы увидеть пики спектра на частотах 240 Гц, 480 Гц и т.д. Однако FFT раскладывает сигнал по другому ряду частот (делим 48000 на 4096): 0 Гц, 11.71875 Гц, 23.4375 Гц и т.д.
Если частота сигнала совпала с одной из базисных частот FFT, то в результате получаем "идеальный" спектр: единственный пик и остальные нули (см. рис. 1, белый). Если же частота сигнала не совпала с базисными частотами FFT, то получаем эффект "размытия спектра": попытка составить синусоиду нужной частоты из множества синусоид других частот (рис. 1, зеленый).
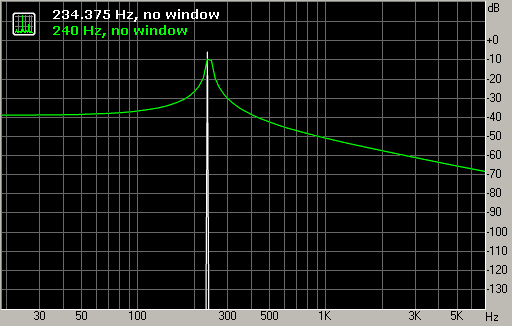
Рис. 1. Размытие спектра для двух синусоид разной частоты с амплитудой -6 dB FS.
Такое размытие спектра в ряде случаев нежелательно: оно может закрывать собой сигнал меньшей амплитуды на других частотах. Для уменьшения эффекта размытия перед вычислением FFT к сигналу применяются т.н. весовые окна, т.е. сигнал домножается на гладкие функции, спадающие по краям отрезка, похожие на гауссиан.
Простейшее окно - прямоугольное, это константа 1, не меняющая сигнала (рис. 1). Это эквивалентно отсутствию весового окна.
Одно из популярных окон - окно Хэмминга. Оно уменьшает уровень размытия примерно на 40 дБ относительно основного пика (рис. 2).
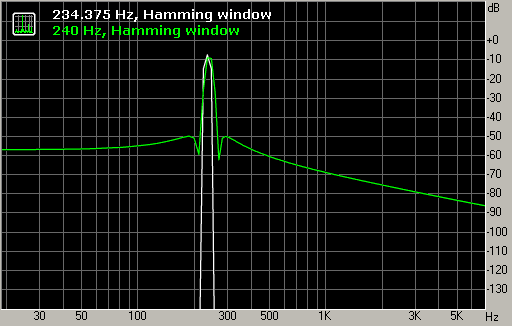
Рис. 2. Окно Хэмминга.
Различные весовые окна отличаются по двум основным параметрам: степени расширения основного пика и степени подавления размытия ("боковых лепестков"). Эти две функции противоположны друг другу: чем сильнее мы хотим подавить размытие, тем шире будет основной пик (см. рис. 3). И наоборот, прямоугольное окно менее всего размывает верхушку пика, но имеет самые высокие боковые лепестки. Окно Кайзера обладает параметром, которые позволяет выбирать нужную степень подавления боковых лепестков.
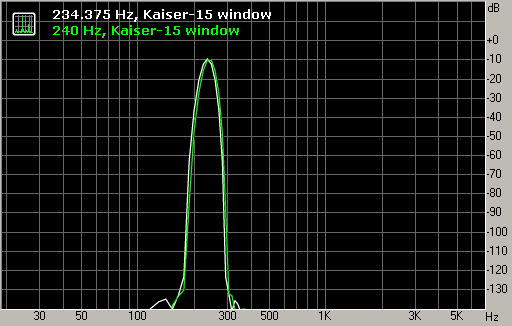
Рис. 3. Окно Кайзера, beta=15.
Другой популярный выбор - окно Хана (Hann), ошибочно называемое Hanning. Оно подавляет максимальный боковой лепесток слабее, чем окно Хэмминга, но зато остальные боковые лепестки быстрее спадают при удалении от главного пика.
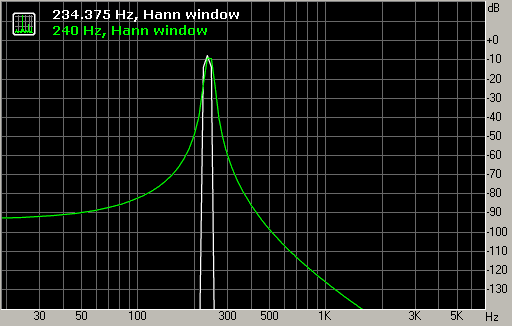
Рис. 4. Окно Хана.
Последнее редактирование:
Окно Блэкмана обладает более сильным подавлением боковых лепестков, чем окно Хана.
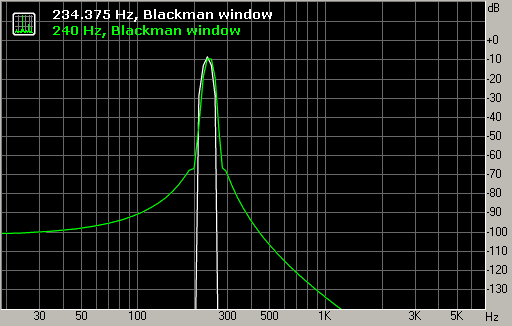
Рис. 5. Окно Блэкмана.
Все рисунки сделаны для синусоид, однако исходя из них нетрудно представить, как будет выглядеть спектр реальных звуковых сигналов. Каждый пик в спектре будет иметь некоторую размытую форму, в зависимости от своей частоты и выбранного весового окна.
Чтобы компенсировать расширение пиков при применении весовых окон, можно использовать более длинные окна FFT: например, не 4096, а 8192 отсчета. Это улучшит разрешение анализа по частоте, но уходшит по времени.
Вывод отсюда такой: для большинства задач не очень важно, какой именно вид весового окна использовать. Главное - чтобы оно было. Популярный выбор - Ханн или Блэкман.
Рис. 5. Окно Блэкмана.
Все рисунки сделаны для синусоид, однако исходя из них нетрудно представить, как будет выглядеть спектр реальных звуковых сигналов. Каждый пик в спектре будет иметь некоторую размытую форму, в зависимости от своей частоты и выбранного весового окна.
Чтобы компенсировать расширение пиков при применении весовых окон, можно использовать более длинные окна FFT: например, не 4096, а 8192 отсчета. Это улучшит разрешение анализа по частоте, но уходшит по времени.
Вывод отсюда такой: для большинства задач не очень важно, какой именно вид весового окна использовать. Главное - чтобы оно было. Популярный выбор - Ханн или Блэкман.
недавно попробовал пингвина только. интерфейс конечно старомодный но программа очень крутая. всё что нужно.
Кто-нибудь пользуется Fre(a)koscope'ом ?
http://mdsp.smartelectronix.com/ffttools/
http://mdsp.smartelectronix.com/doc/index.php/Freakoscope
http://mdsp.smartelectronix.com/ffttools/
http://mdsp.smartelectronix.com/doc/index.php/Freakoscope
Вы точно уже написали про waves paz или осталось немного подшлифовать?
) Спасибо за ссылки на википедию! 
Охренеть :scare: Вот она - блуждающая фабула. На днях сделал мини гайд по анализатором, теперь вижу практически всё то же самое, но написанное ещё до меня... Чувствую себя невольным плагиатором
До недавнего времени пользовался Roger Nichols Digital Inspector XL, в частности Multimeter 2 ch, но вот заметил, что он врёт на где-то на 3 db в +. Сравнивал с измерителями в Samplitude и WaveLab. Печально, он так мне нравится :to_take_umbrage: Но благо есть такие проги , как Pinguin :music2:
ребзя... у меня вопрос...
нужен спектроанализатор которым можно было бы мониторить всё что выходит из DAW на одном и том же компутере. VST мне не подходят
Например если работаю в аблетоне то хочу мониторить выход постоянно даже при переборе сэмплов в браузере аблетона.
Кучу анализаторов перерыл ... у всех только входы аудиокарты указываются ...
Возможно ли вообще такое ???
Надеюсь понятливо обьяснил...заранее спасибо :hi:
нужен спектроанализатор которым можно было бы мониторить всё что выходит из DAW на одном и том же компутере. VST мне не подходят
Например если работаю в аблетоне то хочу мониторить выход постоянно даже при переборе сэмплов в браузере аблетона.
Кучу анализаторов перерыл ... у всех только входы аудиокарты указываются ...
Возможно ли вообще такое ???
Надеюсь понятливо обьяснил...заранее спасибо :hi:
или покупай карту от RME, там есть Диджичек - спектроанализатор, который всегда работает.
У меня почему-то Пингвин не работает с Нюэндо, вто врем как остальное все показывает. Но когда его включаю, начинает звук трещать. Частоты выставлены правильно, что это такое? Может потому, что не ПРО версия Пингвина снимает только 16-битный сигнал?
У меня почему-то Пингвин не работает с Нюэндо, вто врем как остальное все показывает. Но когда его включаю, начинает звук трещать. Частоты выставлены правильно, что это такое? Может потому, что не ПРО версия Пингвина снимает только 16-битный сигнал?
Последнее редактирование:
вроде то что надо ... но не могу заставить работать.... изза настроек ASIO input подвисает сама DAW
Lobz, Александр Жога
есть пингвин....но чтото я не разберусь никак
В Devices опицию Wave Mapper ставить ??? Ничего не показывает... Может в аудиокарте дело?? Карта M-Audio Audiophile 192
зачем????ставим выход своей карты,она у тебя должна в меню dеvice отображаться))
Последнее редактирование:
Да, иногда приходят такие мысли про покупку РМЕ для аналайзера - хороший он там...
А нельзя его как-то переработать, чтобы он работал независимо от карты, как стэдалон? Может кто-то из программистов знает ответ на этот вопрос?)))
странно, у меня там входа отображаются, а не выхода.
EugeneS, Я с Пингвином еле разобрался по подключениям. Не на всех картах можно реализовать, т.к. по умолчанию он работает по входу. Если микшер карты позволяет сделать "внутреннюю петлю" (Loopback), т.е. назначить виртуально воспроизведение на входа лупбека, то тогда он заработает. В девайсах нужно выставить этот вход (накотором лупбек).
Если такой возможности нет, то придется паять перемычку тюльпан-тюльпан и замыкать S/PDIF вход и выход на карте.
Для перемычки купи на радиорынке коаксиальный кабель под пайку (а не обжим), с сопротивлением 75 Ом. Или если не умеешь паять - пиши в ПМ - помогу)
Если ты в Киеве конечно, а не во Флориде)
Последнее редактирование:
Александр Жога,
спасибо ... у меня скорей всего с картой какие то проблемы ...микрофон включенный в карту показывает а остальное нет ) буду разбираться
спасибо ... у меня скорей всего с картой какие то проблемы ...микрофон включенный в карту показывает а остальное нет ) буду разбираться