N
Nible
Guest
Смотрим звук в аттаче.
Полная версия трека
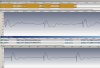
Основной характер звучания лида задает выделенный желтым участок, отмеченное зеленым ничего к звуку лида не добавляет.
Анализ на спектроскопе с минимальным размером окна показывает наличие огибающей на питч, похоже на питч-бас из шляйсовского мануала, но в сабжевом лиде питч уходит вверх.
немного о правильном реверсинге звука:
Многие считают что для повторения звучания достаточно совпадения полученого звука по спектру на экране FFT анализатора. Это применимо для сугубо стационарных периодических сигналов, период которых больше размера окна FFT преобразования. Как правило современные hard звуки настолько накручены LFO, FM, PSK и прочими фишками, что анализ спектра ничего не дает, т.к все переходные процесы усредняются окном в 512 семплов. Выход: использовать осциллограф (осциллоскоп) и спектроскоп с малым размером окна. Но уменьшение размера окна FFT преобразования ведет к уменьшению разрешения по частоте, размер окна 256 сэмплов уже не юзабелен.
P/S сообщения с содержательными с точки зрения СД фразами типа рыба водится в воде и не подкрепленные примерами звука прошу безжалостно удалять.
Полная версия трека
View hidden content is available for registered users!
Основной характер звучания лида задает выделенный желтым участок, отмеченное зеленым ничего к звуку лида не добавляет.
Анализ на спектроскопе с минимальным размером окна показывает наличие огибающей на питч, похоже на питч-бас из шляйсовского мануала, но в сабжевом лиде питч уходит вверх.
немного о правильном реверсинге звука:
Многие считают что для повторения звучания достаточно совпадения полученого звука по спектру на экране FFT анализатора. Это применимо для сугубо стационарных периодических сигналов, период которых больше размера окна FFT преобразования. Как правило современные hard звуки настолько накручены LFO, FM, PSK и прочими фишками, что анализ спектра ничего не дает, т.к все переходные процесы усредняются окном в 512 семплов. Выход: использовать осциллограф (осциллоскоп) и спектроскоп с малым размером окна. Но уменьшение размера окна FFT преобразования ведет к уменьшению разрешения по частоте, размер окна 256 сэмплов уже не юзабелен.
P/S сообщения с содержательными с точки зрения СД фразами типа рыба водится в воде и не подкрепленные примерами звука прошу безжалостно удалять.